Re-expression method is a representation learning method generalized from on a simplistic grammar learning algorithm. The algorithm drives minimum description length (MDL), forces independence of variables and exposes patterns as variables by minimizing description length under independence assumption. In tests the method improved naive Bayesian classification results significantly and the method enabled informative probability estimates with naive Bayesian inference. For example in the Shuttle Control data set the re-expression reduced naive Bayesian error by 97%. Method was used successfully to extract shapes from images and tokens from text, and re-expression of such shapes improved results in naive Bayesian probability inference.

The re-expression problem

Solutions are defined by their problems and the re-expression method is defined by the goal of converting a representation into a more ideal form. In the re-expression problem, the aim is to find for information representation I a more ideal representation I' so that operations on the representation provide more ideal results.

To be able to convert this abstract problem setting into a more formal and exact form, following questions need to be answered: what an ideal expression actually means, what are the very desirable qualities of ideal expression, and is such expression even possible to achieve? Regarding the desired qualities - based on Rissanen minimum description length - the information/model should have minimized information size. Another desired quality is maximum independence of the variables in the information expression, as under independence assumption simplistic compression and naive Bayesian methods do provide ideal compression rates and ideal estimates with ideal performance. Even further, the two qualities around entropy and independence can be optimized via minimizing a single metric, which we may call 'naive entropy, which is the sum of expression's variables' entropies' H_n(I) = H(V₁) + H(V₂) + ... + H(V_k). Minimizing the naive entropy minimizes entropy of the compressed model, while this naive form of entropy reaches true entropy only, if the representation variables reach independence.

The abstract solution

If we split information I into two parts, which are language L and data D so that I = (L, D), we can reframe the problem as finding optimal language learner λ, so that it provide optimal language L' = λ(L, D) and that the new optimal expression I' = (L', D') has minimized naive entropy H_n(I') = H_n(L') + H_n(D').

The abstract solution is following:

Assume independence assumption
Find a condition C in data that is suprisingly common
Form a expression variable E that's true when condition C is true
Add expression variable E into expression. This introduce redundancy, as variable E predicts unambigiously existing variables' states
Eliminate the redundancy by eliminating predicted states from expression. This creates new generation of information I_i+1.
Repeat the process from step 1. for I_i+1

As patterns are eliminated from data they get captured in the language, and the data that once described pixels, letters or variable states becomes data describing also shapes, words, phrases, classes and other patterns.

The implemented solution

This abstract solution can be specialized in a number of different ways. The C++ implementation has following specifics:

(Warning, following information is both dense & complex. I put it here mainly to demonstrate that a solution exists)

All variables and states are binary (e.g. isPixelBlack)
Variables are iterated via context variables, that are vectors of integers, and variables have state for each defined context.
- E.g. context variable Pixel has states (0, 1), (0, 2), ..., (99, 99) and e.g. isPixelBlack((10,10))=true.
Relations R₁, R₂, ..., R_m are used to organize variables and to detect patterns. Relations are of form R(t) = (V_i(t + s_i), V_j(t + s_j), ..., V_k(t + s_k)), where t is context variable state and s_i, ..., s_k are shift vectors, that translate context variable.
- E.g. leftRight(t) = (isPixelBlack(t), isPixelBlack(t + (1,0))) could have value leftRight((10, 10)) = (isPixelBlack((10, 10)), isPixelBlack((11, 10))) = (true, true).
Statistics are gathered per variable and per relation, and they are used to estimate probabilities and statistical dependencies.
- We may have image data of dimensions (100, 100) and so separate statistics based on the 10000 isPixelBlack variable states and based on 9900 leftRight states.
- Statistics may provide e.g. following probabilities for each 4 relation leftRight states: p(leftRight = (true, true))=0.4 and p(leftRight = (false, false)) = 0.5, while other states are present only 10% of time.
For each of the relationship's R state r = (v₁, v₂, ..., v_n), we calculate metric called bias B(r) = n(log (p(v₁) p(v₂) ... p(v_k)) - log p(r)), which is used to detect patterns that break independence assumption.
We scan all relationships' R₁, R₂, ..., R_n states' r₁, r₂, ..., r_m bias values, and pick the relationship R_i state r_j with highest bias B(r_i) as the pattern to eliminate via new expression variable E.
- If the highest state combination r_j bias B(r) is under some threshold T, the process is stopped.
- For the expression variable E it applies that E(t) = true, iff R_i(t) = r_j. E.g. we may have expression variable E(t) that is true, iff leftRight(t)=(true, true)
Introducing E to the information I will also introduce redundancy to the information. This redundancy can be removed by 'eliminating' variable states that can be implictly determined based on following rules:
- The expression rule. E.g. if E((2, 2))=true, then we know that isPixelBlack((2, 2)) and isPixelBlack((3, 2)) must be both true and they can be eliminated, assuming E(t) = isBlackPixel(t)=true AND isBlackPixel(t+(1,0)).
- The expressed state rule. E.g. if E((4, 2))=false, while isPixelBlack((5, 2)) is true, then isPixelBlack((4, 2)) must be false.
- The expression exclusion rule. E.g. if we have expression D(t) <-> upDown(t) = (true, true), and we know E((2, 2)) = true, then we know D((2, 2)), D((2, 1)), D((3, 2)) and D((3, 1)) to be false.
The elimination process is called 'variable reduction process' and it creates variables, which states are eliminated in some contexts and which have different statistical properties than their original versions. The eliminated states are ignored, when building statistics, compressing, classifying or predicting as they are already taken into account via expression variable E.
- E.g. Reduced isPixelBlack is different from original isPixelBlack as it has fewer states and relatively fewer of these states are true

The C++ implementation has also naive Bayesian probability predicter implemented. Once you define data sets and test data, you can use pred::p() method for estimating probabilities for missing variable. A naive compressor that compresses the re-expressed data is also implemented, but unfortunately only for an earlier Java version. Still; the Java compressor using arithmetic encoding did work exactly as predicted compressing the data in naive entropy + epsilon bits, where epsilon was relatively in fourth or fifth decimal. Re-expression improved naive compressor's results as indented; here you have to trust my word, where as the way how naive Bayesian predicting is improved by re-expression is shown on and the results can be reproduced by running the test cases.

Considerations

The nice thing in the C++ implementation is that because context variables and shifts are vectors and all states are binary, it can be hugely optimized with fast bit AND, NOT and POPCOUNT operations. Other very nice aspects are that it provides very good results in classification problems, it provides more or less proper probability estimates, and it is very generic when compared with other existing algorithms.

Still, the solution could be improved in many curious ways. First of all, by varying the way how the original expression of information is defined, you can cover either small set of problems (machine learning, languages), a big set (current solution) or even a bigger range of problem settings, what-ever they may be. This is one level of problem, the low-level information representation. Another level relates relations and expressions or what patterns we can express and how. Current mechanism can only express AND relation between variable states, while OR-like expression is obviously possible. It also seems plausible that some kind of recusion could be learned, where recursion is needed for learning context-free-grammars. One can imagine what context-free-grammars would look like for e.g. images or video. Still, for the re-expression to actually reduce naive entropy of information, one needs to have statistics to detect the patterns and devise a bullet-proff reduction mechanisms for given expression. Statistics and reduction thus form third and fourth levels of re-expression problem. Fifth level of the problem relate to optimizations, like sparse data optimization, which could take the algorithm speed even to another level and parallelization which should be somewhat easy to apply to e.g. heavy operations with statistics. The last level of the problem relate to how statistics are used for probability estimation. While re-expression allows simplistic operations to perform well with data, even these simplistic operations could be greatly improved by developing the mathematics behind the operations.

About Author

Antti Rauhala is a software engineer at Futurice with a passion for artificial intelligence and machine learning. He's also the author of FreeForm meta language.

Results

Following results are for the static C++ library implementing the re-expression method, where the sources can be found at GitHub at https://github.com/arauhala/libreexp/ or downloaded from here. Results can be reproduced by running the library's test suite.

Machine learning samples from StatLog (statlogbits test suite)

StatLog was the comprehensive evaluation of supervised learning from 90s, where 23 methods (including statistical methods, machine learners and neural networks) were evaluated with 29 cases of real world data. Four (4) StatLog data sets were used for testing and comparing re-expression technique against other algorithms:

Data-set	Statlog Rank	Result	(Alt. Result)	Statlog's Best
German credit data	1.	.516	(.496)	.541 (Discrim)
Australian credit data	1.	.128	(.128)	.131 (Cal5)
Heart disease	1.	.344	(.341/.319)	.374 (NaiveBay)
Shuttle control	7.	0.10%	(0.21%)	0.01% (NewId)

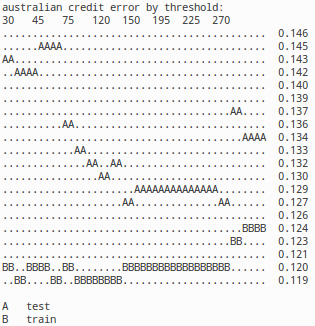
(Alt.Results are for the alternative probabilistic prediction algorithm tried)

First three of the data sets had mostly discrete input data, while fourth contained mainly numerical input. In the three data sets with mostly discrete input, the re-expression+naive Bayesian combo provided the best results. Re-expression technique improved naive Baysian results significantly in the discrete data-sets and dramatically for Shuttle Control by dropping error rate by 30x as visible in following graphs. In graphs smaller threshold means higher level of re-expression, while for entropy, cost and error smaller is better. In German credit, entropy wasn't the StatLog metric, but it's interesting as the best measure for the underlying probability estimate. Results are for both test and train data sets; where test is interesting data set and test/train split follows StatLog instructions.

The graphs here show how various metrics behave, when threshold parameter varies. On the right corner of graph there is typically the result for plain naive Bayes, while on the left side of graph there are results for naive Bayes working on heavily re-expressed data. While re-expression typically helps, too heavy re-expressing will raise granularity of the data too high and lead to undesirable overfitting thus harming the results. What is also visible in the diagrams is that while entropy of predicted variable (see german credit) reduces quite continuously, the cost and error rates may go quite dramatically up and down as re-expression proceeds. This contradicting looking situation is caused by the classification not minding redundancy as long positive and negative evidense is duplicated as many times. If re-expression eliminates duplication indicating A, then also duplication indicating B needs to be eliminated to bring algorithm back to balance.

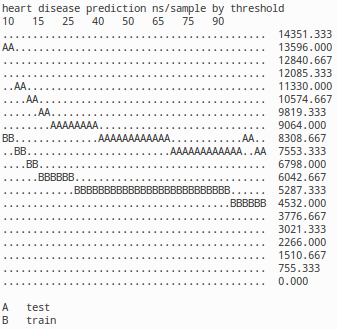
Next graphs demonstrate the algorithm's speed:

Previous images show how the prediction times behave, when the system gets re-expressed. In german credit, australian credit and heart disease samples the prediction speed with re-expressed data stays in the magnitude of plain naive Bayesian predictor. If data is heavily re-expressed, prediction speed may take even twice the time, but per sample the speed remains around 10 microseconds, more or less. As shuttle control data gets re-expressed with much heavier hand, the performance impact is also much bigger, varying between 0.3 ms - 32 us depending of threshold. The learning of re-expression for optimal results took 23 ms for german credit, 92 ms for australian credit, 150ms for heart and 4 seconds for shuttle control. Transforming other data into formed expression is around 50-1000 times faster. Measurements, were done on a single processor of 1.3 Ghz Pentium M netbook.

Images and image classification (image, optdigits test suites)

So, re-expression technique does give major boost to naive Bayesian classifier in more traditional machine learning problems. But how does the algorithm work with different kind of data, like images. Here I'll present two problem settings, where first is about parsing an image into its graphical primitives.

In the first problem setting, we have a screenshot of the classic game 'Space Invaders', shown left. Here learning 108 expressions from the 54k pixels took 3.7 seconds. The expressions were sorted based on how many of them were found in the image and that how much information they carry and the picture on the right visualizes the top 15 expressions from that list. For each shown expression exists a bit vector showing the exact locations, where the monsters, ships or letters are present in the image. Because re-expressing is extremely fast once the new expression has been learned, the technique could be used out-of-box for parsing real-time stream of Space Invaders' pixels, or parsing the pixels out of similar old game classics.

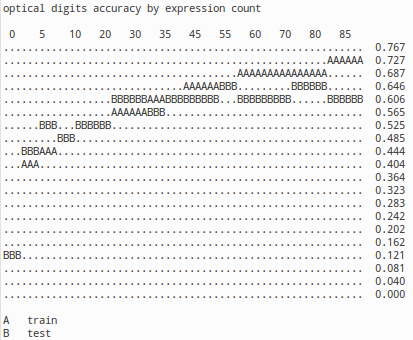
The second problem setting combines pattern recognition in images with classic machine learning. The data set 'Optical Recognition of Handwritten Digits' is from UCI machine learning repository, where there are 32x32 bit images of hand written digits. The set is split into few sets, of which we use train set of 1934 images and validation set of 946 images. The image on left shows how classification accuracy behaves, when more expressions are added. It is worth noting that the algorithm doesn't utilize the location information for pixels. The naive version of classification therefore merely counts pixels and tries to deduce class by pixel count, which results meager 14% accuracy. Once expression count is raised to 80, the accuracy raises to 0.650, which isn't very impressive, but it shows that out-of-box re-expression mechanism does its job. Results would likely greatly improve, if location information was taken into account. Image on right visualizes how digits are parsed into primitive shapes that are then used to predict the digit based on statistics.

Because the problem setting of previous test case is quite excotic, it doesn't provide good or comparable results for the optdigits data sets. More comprarable test case was also created, which results can be found from here. While the results of this data set are neither super impressive, the plain naive bayesian did provide error rate of 0.103 and re-expression did drop the error to 0.055 (with 500 expressions), which means 47% reduction in error. In this way, the used naive Bayesian provided comparable rates to naive Bayesian results found in public and re-expression technique did deliver major improvement, even if KNN and certain kinds of decision trees can apparently provide much better results for this specific data.

Generic tests for machine learning (vars test suite)

In vars test suite, there are separate tests for simplistic AND, OR and XOR relationships, but even further there are test cases, where input-to-input variable and input-to-output variable dependencies are each randomized based on configurable average dependencies. This rather generic test setting is useful for testing some core assumptions of the re-expression technique tat are 1) elimination of redundancy reduces bias thus improving naive Bayesian results and 2) re-expression+naive Bayesian combo provides valid probabilities that can be treated as probabilities. Even futher we would like to know, whether the estimated probabilities converge to the real probabilities given enought data.

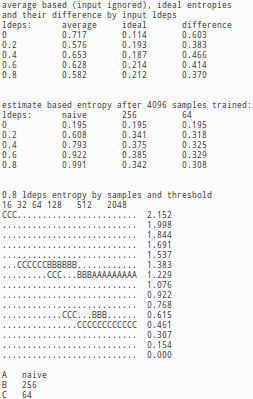
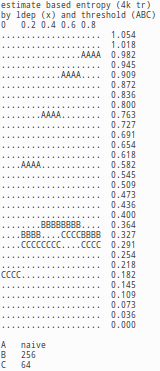
Because we are trying to estimate accuracy of probabilties, we measure the results with a version Shannon's information entropy, which measures in how many bits the variable can be encoded on average using the estimated probabilities. As we know the system generating the information, we can calculate also 'ideal entropy' that is the best possible result (lower is better) and what we might call 'variable naive entropy', which is based on the variable states alone ignoring the input data. Difference between these values describe that how much information input variables contain of the predicted variable. In the test setting there was 64 input variables with varying average dependency and up to 4096 trained samples. The results are based on 200 predictions on 20 different randomly generated systems for each threshold and sample count combination.

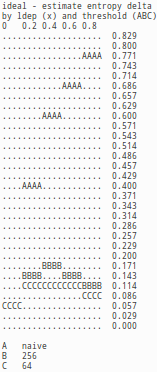The tables and images demonstrate well the pathological behavior of the naive Bayesian inference, when input variables are dependent. Even with smallest measured redundancy (ldep=0.2) in input, the naive bayesian inferences performs worse (0.608) than the naive estimate (0.576) that simply ignores entire input. The fact that naive Bayesian inference provides garbage with even smaller redundancy explains why method is generally not used for estimating probabilities, but instead as a classifier. As input variables get more redundant, the naive Bayesian biases and probabilities become even wilder, while the behavior is completely different if data is re-expressed. If re-expression is applied, the probabilities are informative and even accurate. Even further the difference between estimate based and ideal entropy does not greatly depend of ldep indicating that the re-exression aided predicting works regardless of redundancy in input.

The results do give indication, that the probability estimates for re-expression supported predictor would converge towards the ideal, in the case of our test. While the testing does not progress far enought to really verify or falsify this claim, even if the results do consistently improve up to 4096 samples, the resuls make it obvious that with enought samples the provided probabilities are real probabilities and even pretty accurate probabilities and they can be treated as such. Of course, the amount of the required samples to reach this desirable condition varies depending of variable count, redundancy in the system and the threshold.

Language learning and world learning (text, rooms test suites)

There are several other test cases in the re-expression library's test suite, which may not be super-impressive, but which are interesting anyway. One reason, why all tests are not very impressive has been simply the lack of time in creating more challenging and complete test cases. Another reason as in case of 'rooms' is the inherent complexity in the data. Few test cases in 'text' test suite is around learning grammar for very simplistic pieces of text and finding correct classification (bear or pirate). Another test case has generated text and the problem is detecting the class of the text generator. Third test case treated simply the lang.h file found among the sources and the recognized tokens of the code can be found in here

There is also one complete different kind of test called 'rooms', which deals with a very simplistic game, where the player needs to escape from dungeon with one to two room and with 5x5 view of the surrounding map tiles. The data set consist of logs of 200 games of up to 20 turns with variables describing the game end result, turn situation and the 25 visible tiles. The goal is to model the consequence of decisions and that what kind game situation predicts victory. In a way, the problem is the problem of modeling 1) the entire game world 2) decisions 3) heuristics (goals and how to achieve them) and 4) relationships between these things. In this way, the rooms problem is the McCarthy's epistomological problem in a miniature form. The data is organized into 4 dimension space (game, turn, x, y) and it contains information around tiles (is wall, light, stair), decisions and utility value (game won). The relationships between variables make it possible to detect shapes that are 3 dimensional (time*x*y) and associate these with the many variables. In principle, patterns of isWall(g, t, x, y) AND moveLeft(g, t) AND isWall(g, t+1, x+1, y) can be detected throught relationships and these patterns would work to detect 1) how the world works 2) what leads to victory and 3) behavioral routines in general and in certain conditions. At some level the intended kind of learning does occur, but the results are mixed and not very impressive. The most impressive part is merely how potent the language of variables, context vector and relationships is in describing 'nethack' kind of worlds and that the engine is able to consume the 200 games of up to 20 turns, 25 pixels and tens of variables and learn some patterns in few ten seconds. Still, while the techniques and test cases can be - with no doubt - improved: right now the test setting does not provide useful results.